
Pengertian laju rata-rata adalah total jarak per total waktu. Menghitung laju rata-rata biasanya akan di cari dulu waktu untuk masing-masing laju, menggunakan jarak, lalu dibagi dengan waktu totalnya. Sedangkan pengertian rata-rata harmonik adalah rata-rata yang dihitung dengan cara mengubah semua data menjadi pecahan, dimana nilai data dijadikan sebagai penyebut dan pembilangnya adalah satu, kemudian semua pecahan tersebut dijumlahkan dan selanjutnya dijadikan sebagai pembagi jumlah data.
Untuk lebih mudah menghitung laju rata-rata dengan cara rata-rata harmonik, Ahmad-Ridwan Tresna Nugraha, sewaktu menjadi mahasiswa S3 bidang fisika teori zat padat di Tohoku University, Jepang, menulis tentang “rata-rata harmonik” di Majalah Guru1000.
Misalkan kita menempuh perjalanan PP (“pergi-pulang” atau “pulang-pergi”) dari Sabang sampai Merauke. Perjalanan “pergi” dilakukan dengan laju 15 km/jam, sedangkan perjalanan “pulang” dengan laju 30 km/jam. Kemudian muncul pertanyaan,
“Berapa laju rata-rata perjalanan PP tersebut?”
Dengan sangat percaya diri, mungkin kita langsung menjawab, (15 + 30)/2 = 22.5 km/jam.
Benarkah jawaban tersebut?
Jawaban itu salah! Mari kita telaah lagi. Banyak di antara kita menjawab demikian karena menganggap tiap komponen laju memiliki “bobot” yang sama terhadap laju rata-rata. Perlu disadari bahwa tidak selamanya komponen penyusun nilai rata-rata semuanya memiliki bobot yang sama. Seperti pertanyaan laju rata-rata ini, dua laju yang berbeda menghasilkan waktu tempuh yang berbeda pula.
Untuk jarak yang sama, laju 30 km/jam memiliki waktu tempuh yang lebih singkat dibanding 15 km/jam. Jawaban yang tepat untuk pertanyaan laju rata-rata ini adalah dengan memandang nilai 15 km/jam memiliki bobot 2 kali lebih besar daripada 30 km/jam karena waktu tempuh perjalanannya yang dua kali lebih lama. Dengan demikian, laju rata-rata yang benar adalah:
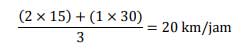
Jika kita tidak begitu yakin jawabannya seperti itu, cobalah tinjau contoh lain yang lebih “merakyat”. Misalkan ada seorang siswa yang mengikuti sepuluh ujian fisika dalam satu semester. Sembilan dari tes yang diikutinya bernilai 100, sedangkan satu tes sisanya bernilai 50. Apakah adil jika nilai rata-rata siswa tersebut adalah (100 + 50) / 2 = 75? Tentu tidak!
Perhitungan nilai rata-rata yang adil untuk siswa itu adalah dengan terlebih dahulu mengalikan setiap nilai terhadap “bobot”nya masing-masing, yaitu seberapa banyak nilai tersebut diperoleh. Jadi, nilai rata-rata sang siswa adalah
Sekarang kita kembali ke persoalan laju rata-rata. Seorang yang memiliki rasa penasaran tinggi mungkin akan bertanya,
“Bagaimana jika salah satu laju itu bukan kelipatan dari yang lainnya?”
Ada cara yang lebih efisien untuk menghitung laju rata-rata tersebut. Di sini kita akan menggunakan konsep rata-rata harmonik, yaitu rata-rata dari barisan harmonik. Istilah “harmonik” boleh dianggap berasal dari pola bilangannya: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, dan seterusnya. Jika kita membuat sebuah gitar dengan panjang relatif satu senar dengan senar lainnya seperti itu, maka akan muncul alunan melodi indah nan harmonis.
Kesalahpahaman terhadap konsep nilai rata-rata biasanya menyebabkan kebingungan yang amat sangat. Untuk menghindarinya, sekali kita tahu bahwa kita sedang ingin menghitung laju rata-rata (dengan cara rata-rata harmonik), maka kita akan punya rumusan yang sangat menyenangkan dalam perhitungan rata-rata harmonik untuk laju-laju dengan jarak yang sama.
Pada soal yang kita bahas di awal, jarak yang ditempuh dengan masing-masing laju adalah sama, yaitu jarak antara Sabang dan Merauke. Di bawah ini diberikan langsung rumus jadinya, coba turunkan sendiri.
Untuk dua laju a dan b, rumus nilai rata-ratanya adalah:
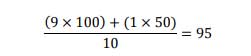
Begitu pun seterusnya. Polanya sangat jelas, bukan? Terapkan rumus rata-rata harmonik ini pada soal awal yang kita berikan, untuk dua laju a = 15 km / jam dan b = 30 km/jam:

Kita coba soal lain yang lebih susah.
Biasanya sebuah angkutan kota (angkot) melakukan perjalanan PP dari Bogor ke Depok lalu balik lagi dari Depok ke Bogor dengan laju rata-rata 300 km/jam. Esok harinya, ada angin yang berhembus dengan laju 50 km/jam dari Bogor ke Depok. Apabila kita anggap bahwa kelakuan supir angkot itu tetap sama, bagaimana laju rata-rata perjalanan PP-nya pada hari tersebut setelah adanya angin? Apakah lebih cepat? Lebih lambat? Atau sama saja?
Dengan pikiran selintas tanpa menggunakan rumus rata-rata harmonik, kita mungkin berpikir sama saja. Asumsinya adalah angkot tersebut mendapat “bantuan” angin pada jalur Bogor ke Depok (jadi lajunya 350 km/jam), sedangkan pada jalur Depok ke Bogor mendapat “hambatan” angin (jadi lajunya 250 km/jam).
Dengan pola pikir yang keliru seperti di awal tulisan ini, didapatkanlah laju rata-ratanya (350 + 250)/2 = 300 km/jam. Hasilnya sepintas sama saja. Tapi coba terapkan rumus rata-rata harmonik,
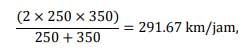
ternyata lebih lambat! Dan inilah hasil yang benar. Coba juga rumus rata-rata harmonik untuk data lain yang lebih banyak nilainya, tidak hanya dua nilai.
Bahan bacaan:
- http://102fm-itb.org/2008/07/miskonsepsi-laju-rata-rata/







